Gaussian Mixture Models
The evils of “hard” assignments
The evils of “hard” assignments
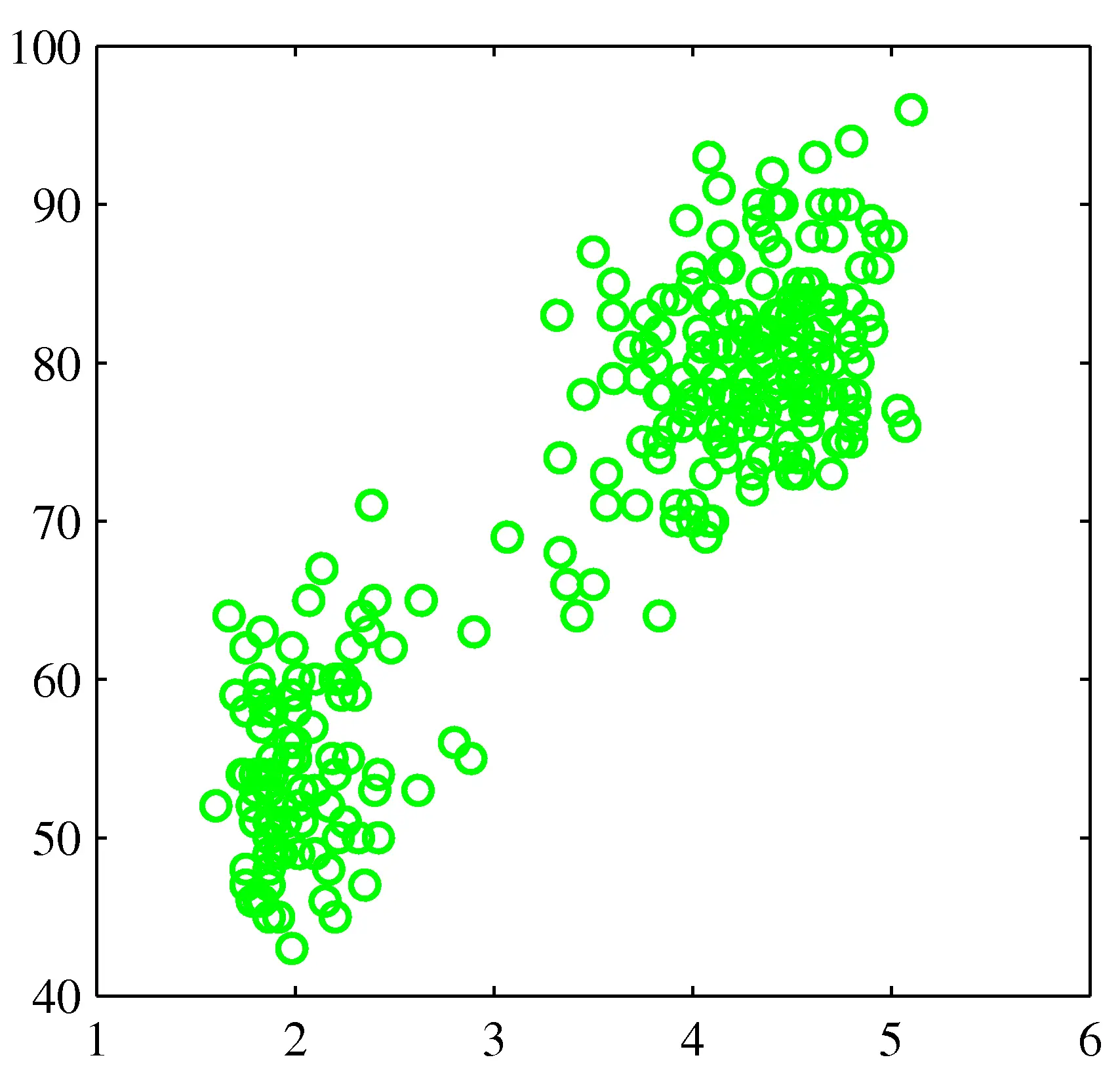
- Clusters may overlap
- Some clusters may be “wider” than others
- Distances can be deceiving!
Probabilistic clustering
- Try a probabilistic model!
- Allows overlaps, clusters of different size, etc.
- Can tell a generative story for data
- \(P(X\mid Y) P(Y)\)
- “What is the probability of points, given what we have observed?”
- Challenge: need to estimate model parameters without labeled
Ys
Probabilistic clustering
| Y | \(X_1\) | \(X_2\) |
|---|---|---|
| ?? | 0.1 | 2.1 |
| ?? | 0.5 | -1.1 |
| ?? | 0.0 | 3.0 |
| ?? | -0.1 | -2.0 |
| ?? | 0.2 | 1.5 |
| … | … | … |
The general GMM assumption
- \(P(Y)\): There are k clusters/components
- \(P(X\mid Y)\): Each component generates data from a multivariate Gaussian with mean \(\mu_i\) and covariance matrix \(\Sigma_i\)
Each data point is sampled from a generative process:
- Choose component i with probability \(P(y=i)\)
- Generate datapoint \(N(m_i, \Sigma_i)\)
What model should we use?
- Depends on X.
- If we know which points are in a cluster, then we can define the best distribution for it.
- Multinomial over clusters Y
- (Independent) Gaussian for each \(X_i\) given Y
\[p(Y_i = y_k) = \theta_k\]
\[P(X_i = x \mid Y = y_k) = N(x \mid \mu_{ik}, \sigma_{ik})\]
Could we make fewer assumptions?
- What if the \(X_i\) co-vary?
- What if there are multiple peaks?
- Gaussian Mixture Models!
- \(P(Y)\) still multinormal
- \(P(\mathbf{X}\mid Y)\) is a multivariate Gaussian distribution:
\[P(X = x_j \mid Y = i) = N(x_j, \mu_i, \Sigma_i)\]
Multivariate Gaussians
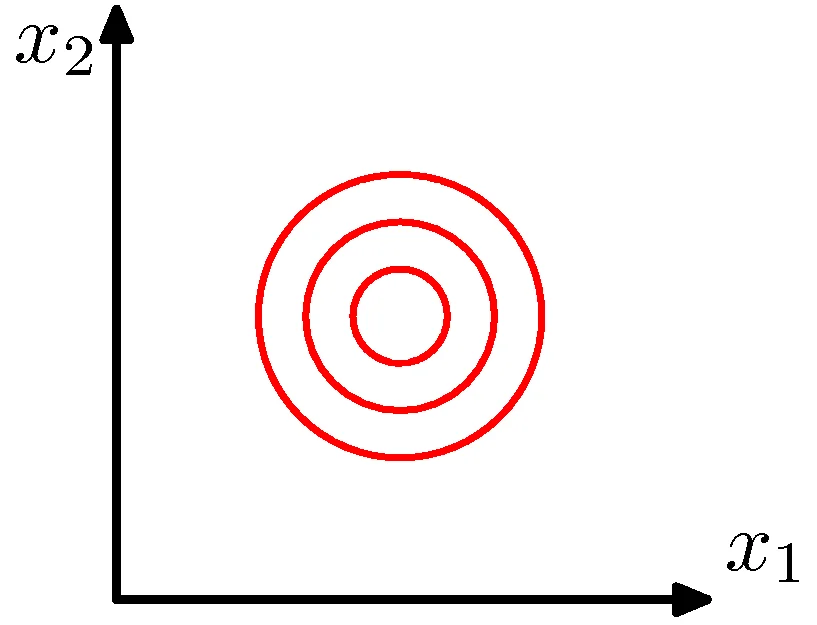
Circular distribution
\[P(X=\mathbf{x}_{j})=\frac{1}{(2\pi)^{m/2}\|\Sigma\|^{1/2}}\exp\left[-\frac{1}{2}(\mathbf{x}_{j}-\boldsymbol{\mu})^{T}\Sigma^{-1}(\mathbf{x}_{j}-\boldsymbol{\mu})\right]\]
\(\Sigma\) is the identity matrix
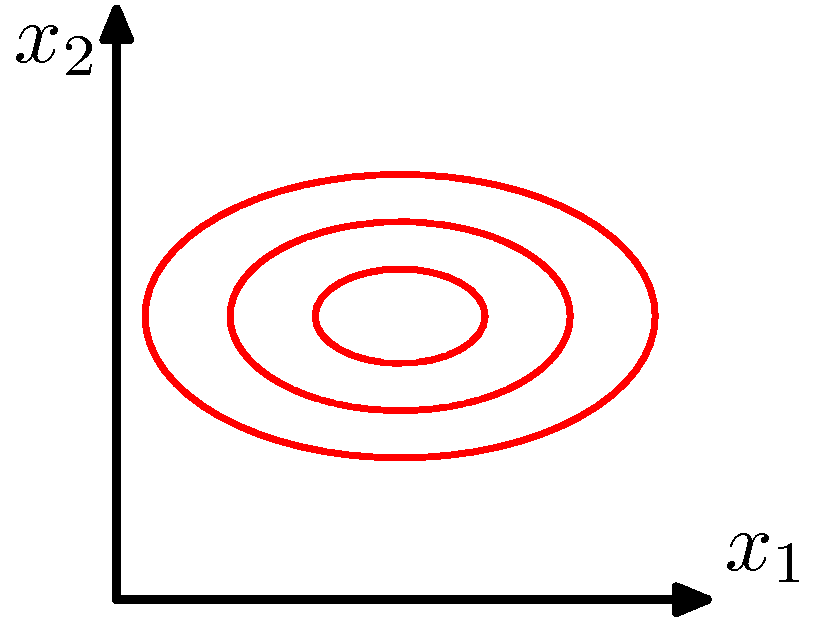
Ovals!
\[P(X=\mathbf{x}_j) = \frac{1}{(2\pi)^{m/2} \|\Sigma\|^{1/2}} \exp\left[-\frac{1}{2}(\mathbf{x}_j - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x}_j - \boldsymbol{\mu})\right]\]
\(\Sigma\) is a diagonal matrix
\(X_i\) are independent and uncorrelated
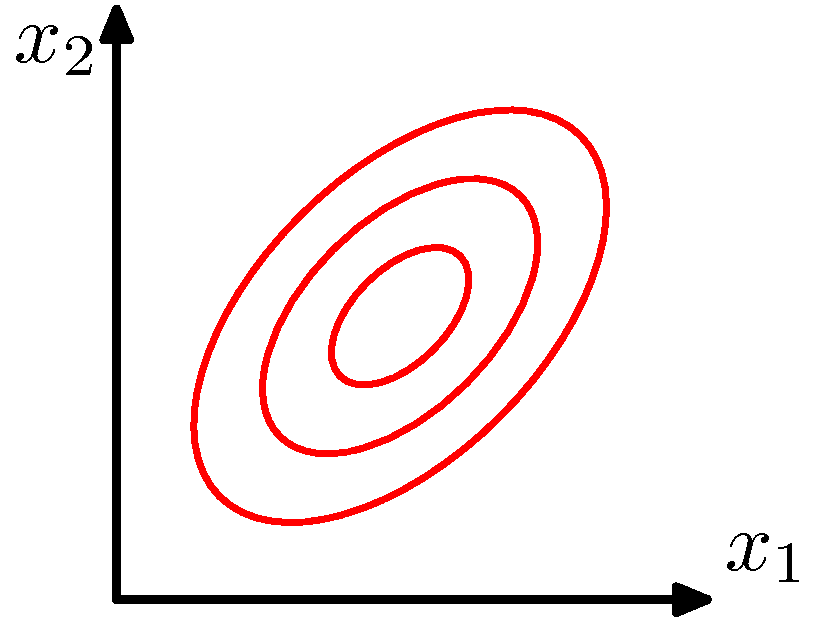
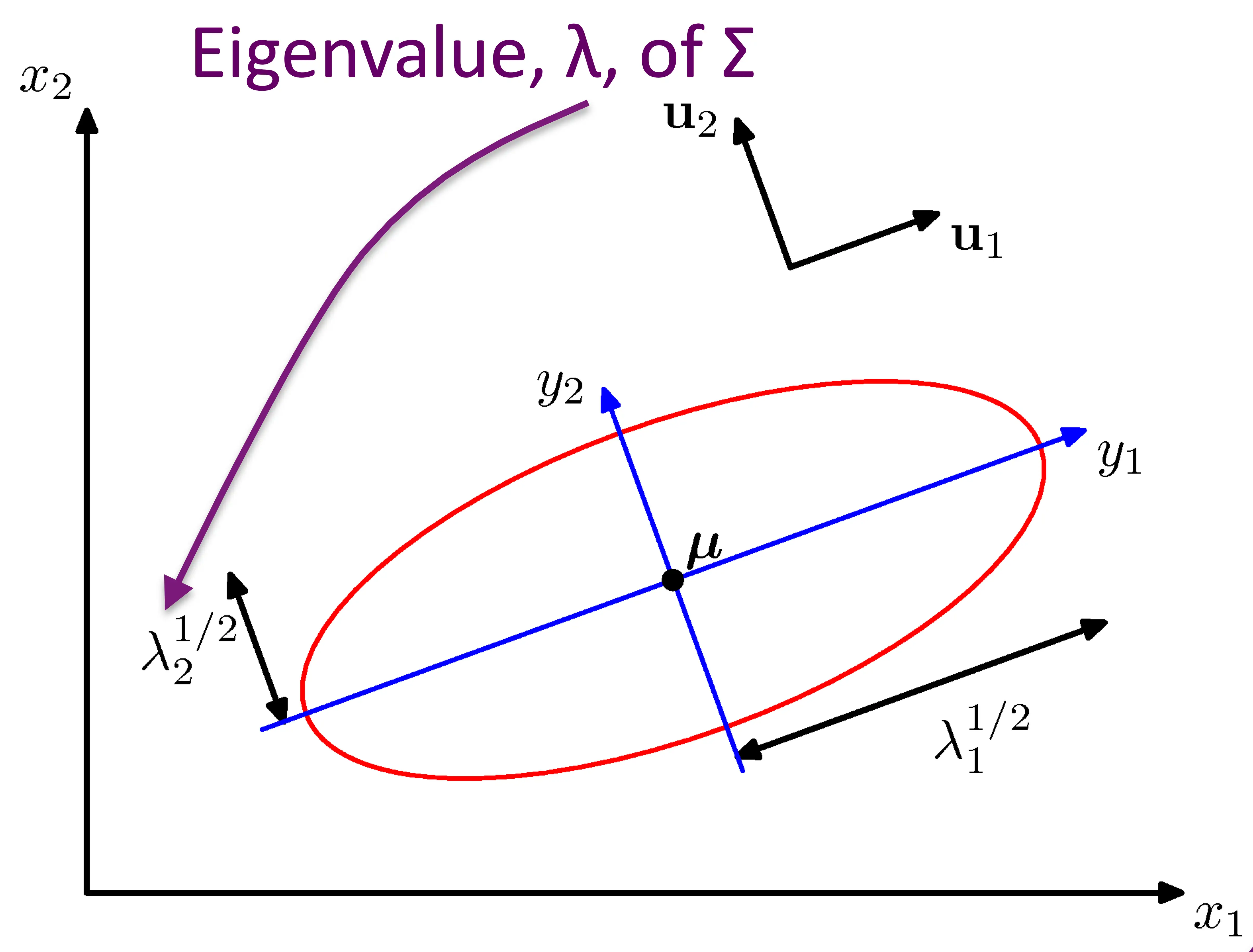
General case
\[P(X=\mathbf{x}_j) = \frac{1}{(2\pi)^{m/2} \|\Sigma\|^{1/2}} \exp\left[-\frac{1}{2}(\mathbf{x}_j - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x}_j - \boldsymbol{\mu})\right]\]
\(\Sigma\) is an arbitrary (semidefinite) matrix
Specifies rotation/change of basis
Eigenvalues specify the relative elongation
\(\Sigma\) accounts for degree to which points vary together
\[P(X=\mathbf{x}_j) = \frac{1}{(2\pi)^{m/2} \|\Sigma\|^{1/2}} \exp\left[-\frac{1}{2}(\mathbf{x}_j - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x}_j - \boldsymbol{\mu})\right]\]
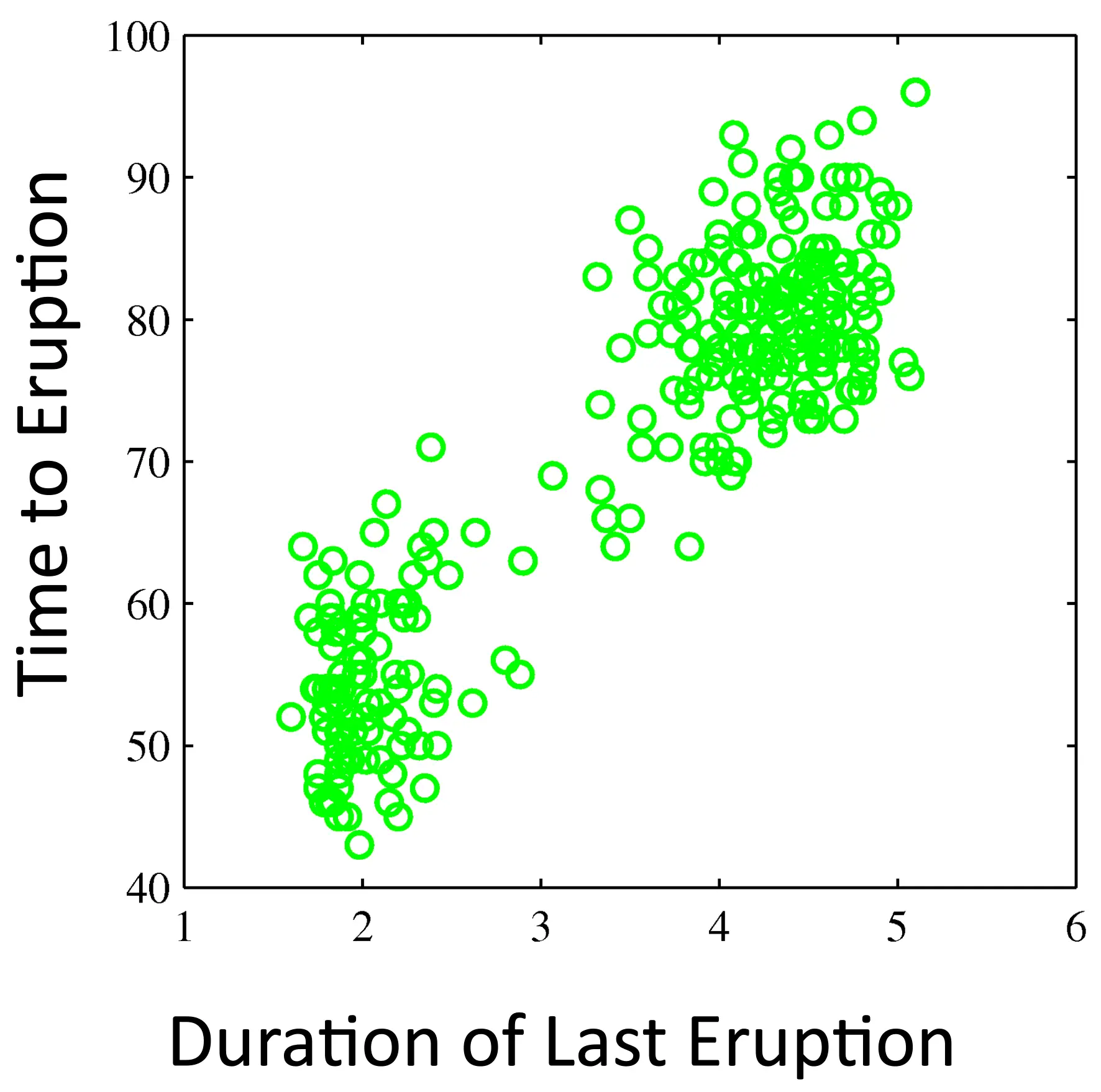
How can we even more flexibly fit distributions?
Old Faithful Data Set
Two distributions might fit the data better
Old Faithful Data Set
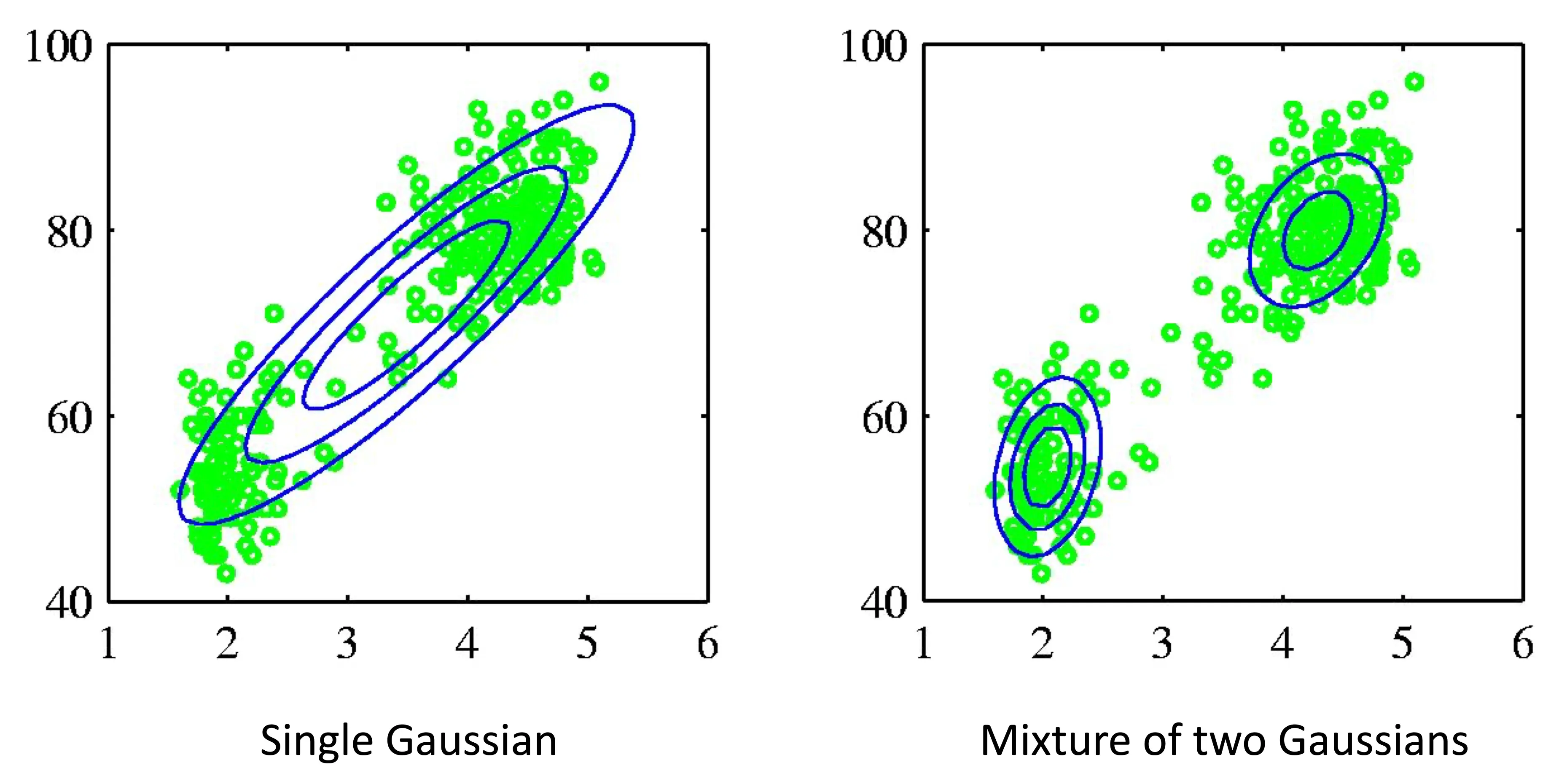
We can make mixtures of distributions!
Combine simple models into a complex model:
\[p(\mathbf{x}) = \sum_{k=1}^K \pi_k \mathcal{N} (\mathbf{x} | \boldsymbol{\mu}_k, \mathbf{\Sigma}_k)\]
\[\forall k: \pi_k \geq 0\]
\[\sum_{k=1}^K \pi_k = 1\]
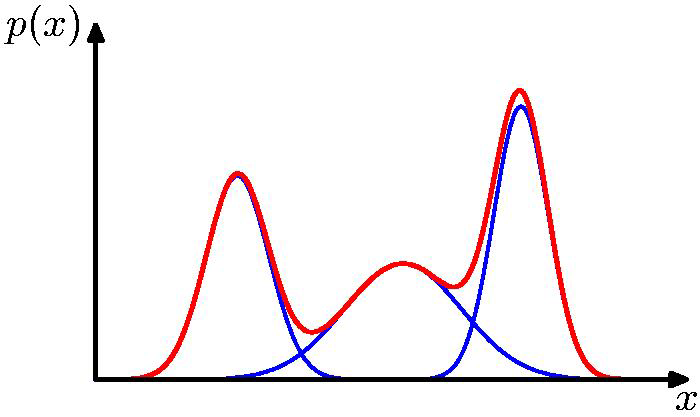
Distribution mixtures eliminate hard assignments
Model data as mixture of multivariate Gaussians
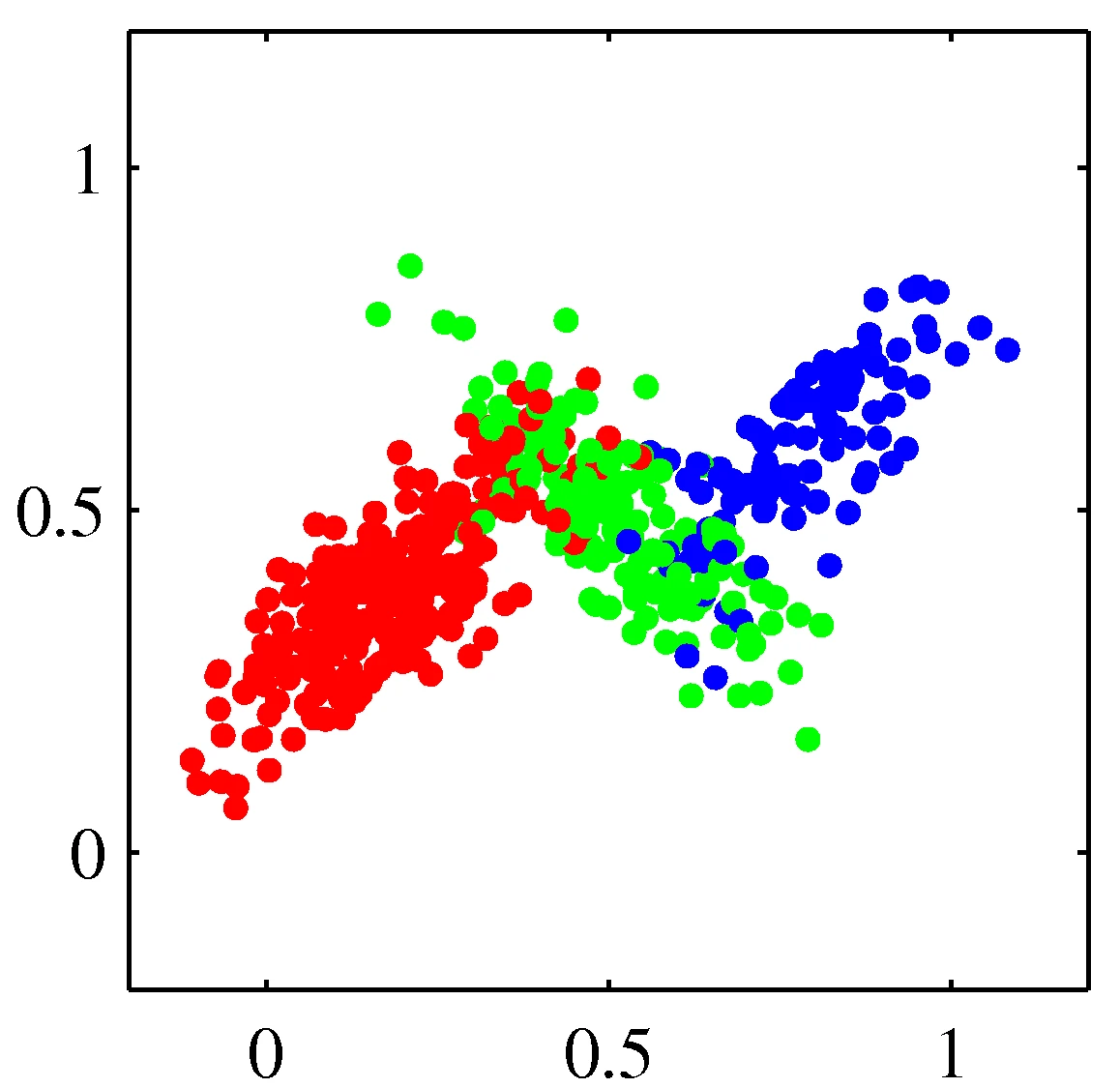
Distribution mixtures eliminate hard assignments
Model data as mixture of multivariate Gaussians
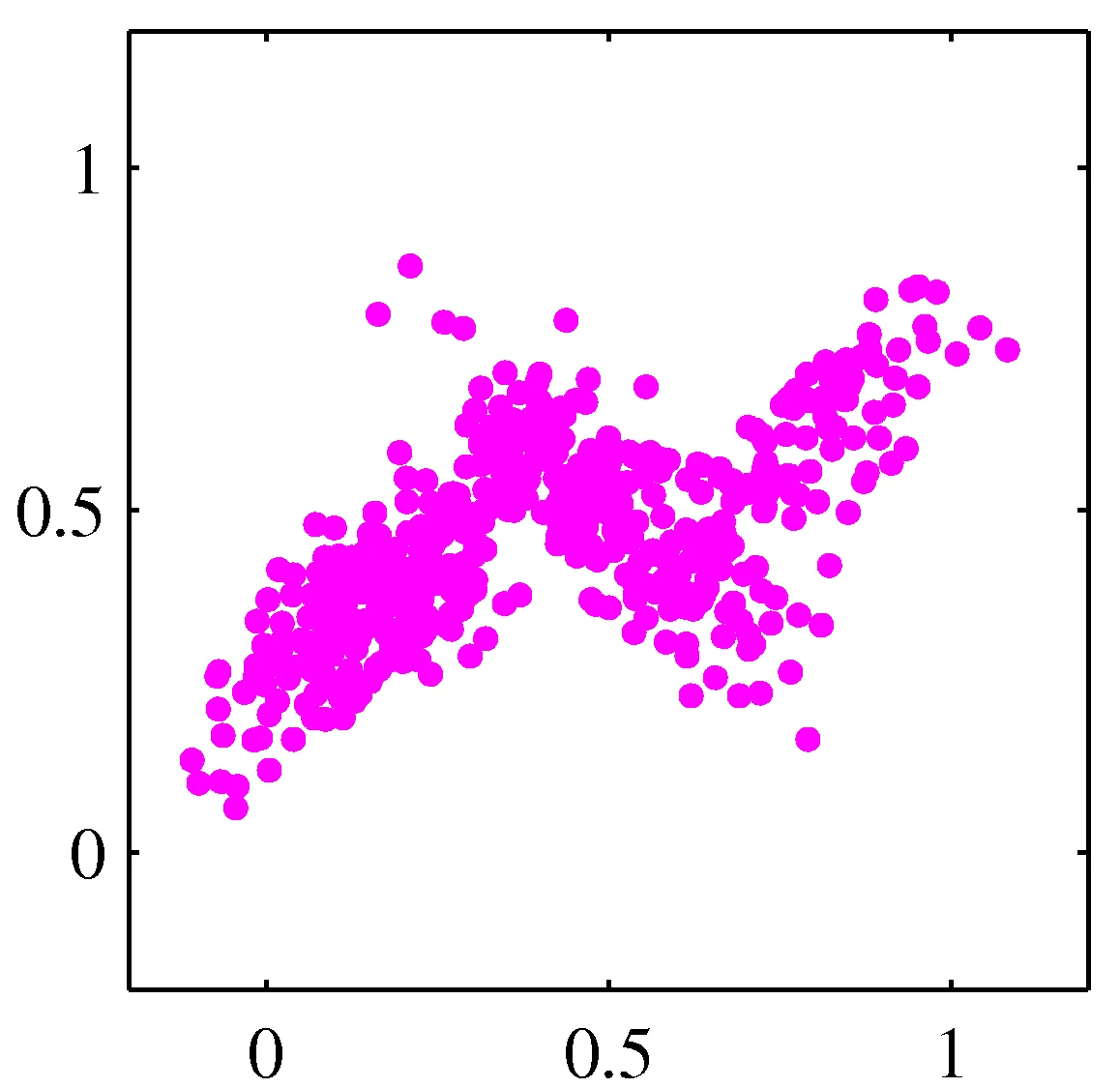
Distribution mixtures eliminate hard assignments
Model data as mixture of multivariate Gaussians
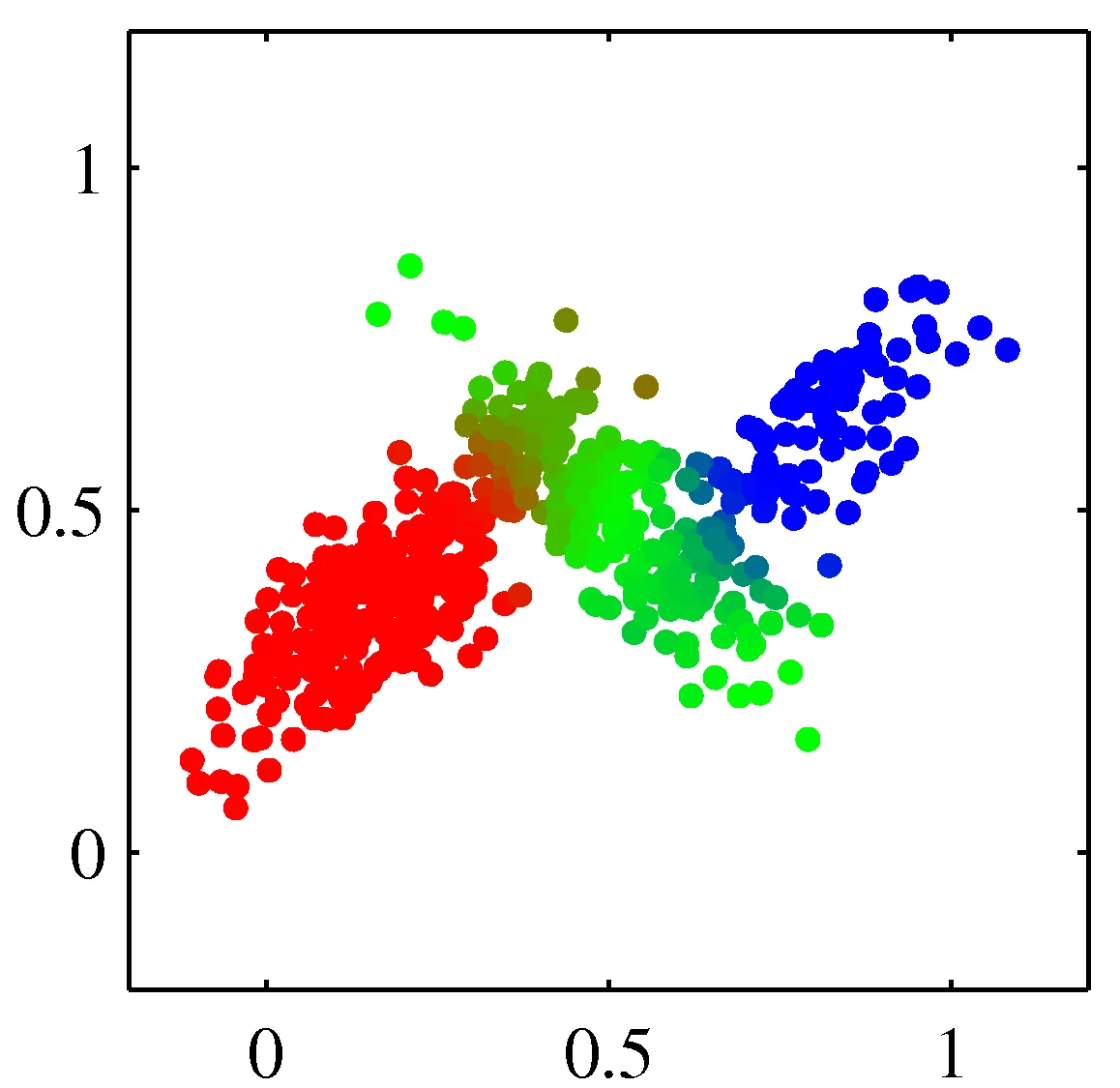
Shown is the posterior probability that a point was generated from \(i\)th Gaussian: \(Pr(Y = i \mid x)\)
Fitting in a supervised setting
Univariate Gaussian
\[\mu_{MLE} = \frac{1}{N}\sum_{i=1}^N x_i \quad\quad \sigma_{MLE}^2 = \frac{1}{N}\sum_{i=1}^N (x_i -\hat{\mu})^2\]
Mixture of Multivariate Gaussians
ML estimate for each of the Multivariate Gaussians is given by:
\[\mu_{ML}^k = \frac{1}{n} \sum_{j=1}^n x_n \quad\quad \Sigma_{ML}^k = \frac{1}{n}\sum_{j=1}^n \left(\mathbf{x}_j - \mu_{ML}^k\right) \left(\mathbf{x}_j - \mu_{ML}^k\right)^T\]
Sums over \(x\) generated from the \(k\)’th Gaussian
But what if unobserved data?
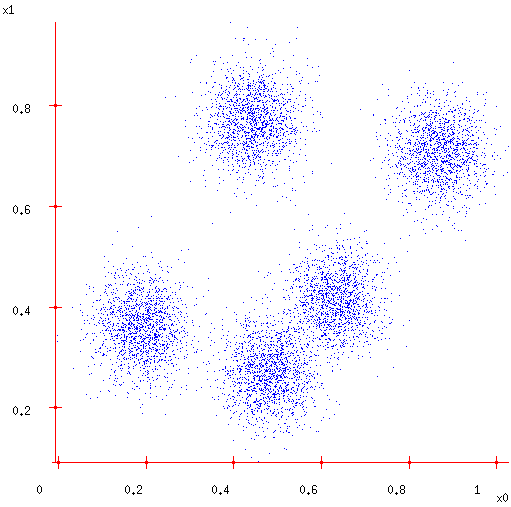
But what if unobserved data?
- MLE: \(\arg\max_\theta \prod_j P(y_i, x_j)\)
- \(\theta\): all model parameters
- e.g., class probs, means, and variances
- But we don’t know \(y_j\)’s!
- \(\theta\): all model parameters
- Maximize marginal likelihood:
- \(\arg\max_\theta \prod_j P(x_j) = \arg\max_\theta \prod_j \sum_{k=1}^K P(Y_j=k, x_j)\)
How do we optimize? Closed Form?
- Maximize marginal likelihood: \[\arg\max_{\theta} \prod_j P(x_j) = \arg\max \prod_j \sum_{k=1}^K P(Y_j=k, x_j)\]
- Almost always a hard problem!
- Usually no closed form solution
- Even when lgP(X,Y) is convex, lgP(X) generally isn’t…
- For all but the simplest P(X), we will have to do gradient ascent, in a big messy space with lots of local optima…
Learning general mixtures of Gaussians
\[P(y = k | \mathbf{x}_j) \propto \frac{1}{(2\pi)^{n/2} ||\Sigma_k||^{1/2}} \exp\left[-\frac{1}{2}(\mathbf{x}_j - \mu_k)^T \Sigma_k^{-1}(\mathbf{x}_j - \mu_k)\right]P(y = k)\]
Marginal likelihood: \[\prod_{j=1}^m P(\mathbf{x}_j) = \prod_{j=1}^m \sum_{k=1}^K P(\mathbf{x}_j, y = k)\] \[= \prod_{j=1}^m \sum_{k=1}^K \frac{1}{(2\pi)^{n/2} ||\Sigma_k||^{1/2}} \exp\left[-\frac{1}{2}(\mathbf{x}_j - \mu_k)^T \Sigma_k^{-1}(\mathbf{x}_j - \mu_k)\right]P(y = k)\]
Need to differentiate and solve for \(\mu_k\), \(\sum_k\), and P(Y=k) for k=1..K
There will be no closed form solution, gradient is complex, lots of local optimum
Wouldn’t it be nice if there was a better way!?!
Expectation Maximization
The EM Algorithm
- A clever method for maximizing marginal likelihood:
- \(\arg\max_{\theta} \prod_j P(x_j) = \arg\max_{\theta} \prod_j \sum_{k=1}^K P(Y_j=k, x_j)\)
- A type of gradient ascent that can be easy to implement
- e.g. no line search, learning rates, etc.
- Alternate between two steps:
- Compute an expectation
- Compute a maximization
- Not magic: still optimizing a non-convex function with lots of local optima
- The computations are just easier (often, significantly so!)
- Especially useful when the E and M steps have closed form solutions!
Simple(r) example: learn means only!
Consider:
- 1D data
- Mixture of k=2 Gaussians
- Variances fixed to \(\sigma=1\)
- Uniform distribution over classes
- Just need to estimate \(\mu_1\) and \(\mu_2\)
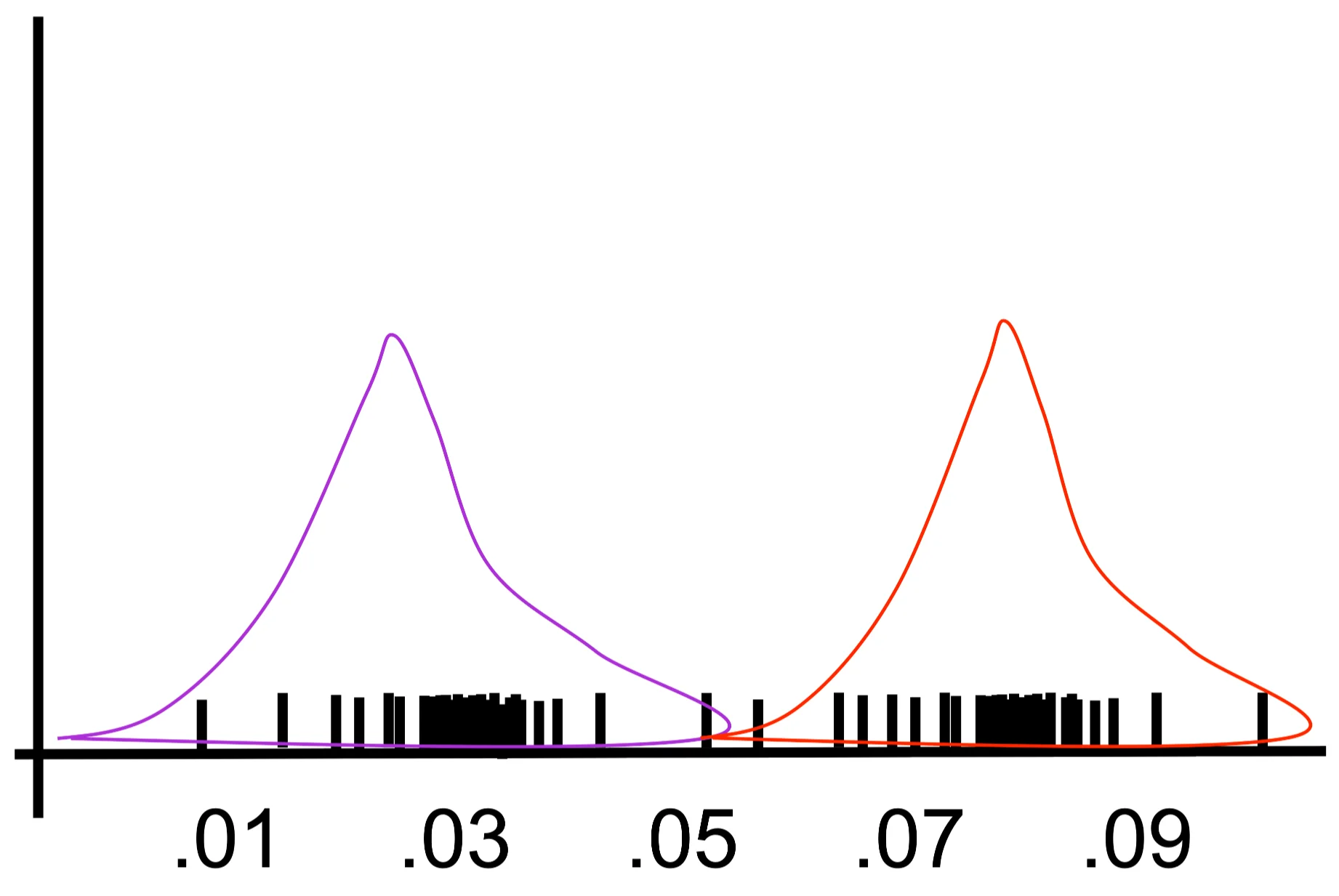
\[ \prod_{j=1}^{m}\sum_{k=1}^{K} P(x,Y_{j} = k) \propto \prod_{j=1}^{m}\sum_{k=1}^{K=2}\exp\left[-\frac{1}{2\sigma^{2}} \| x - \mu_{k} \|^{2}\right] P(Y_{j}=k) \]
EM for General GMMs
General GMMs: Setup
Iterate: On the \(t\)’th iteration let our estimates be
\[ \lambda_t = \{ \mu_1^{(t)}, \mu_2^{(t)} ... \mu_K^{(t)}, \Sigma_1^{(t)}, \Sigma_2^{(t)} ... \Sigma_K^{(t)}, p_1^{(t)}, p_2^{(t)} ... p_K^{(t)} \} \]
\(p_k^{(t)}\) is shorthand for estimate of \(P(y=k)\) on \(t\)’th iteration
General GMMs: E-step
Compute “expected” classes of all datapoints for each class
\[ P(Y_j = k|x_j, \lambda_t) \propto p_k^{(t)}p(x_j|\mu_k^{(t)}, \Sigma_k^{(t)}) \] Just evaluate a Gaussian at \(x_j\)
General GMMs: M-step
Compute weighted MLE for \(\mu\) given expected classes above
\[ \mu_k^{(t+1)} = \frac{\sum_j P(Y_j = k|x_j,\lambda_t)x_j}{\sum_j P(Y_j = k|x_j,\lambda_t)} \]
\[ \Sigma_k^{(t+1)} = \frac{\sum_j P(Y_j = k|x_j,\lambda_t) [x_j - \mu_k^{(t+1)}][x_j - \mu_k^{(t+1)}]^T}{\sum_j P(Y_j = k|x_j,\lambda_t)} \]
\[ p_k^{(t+1)} = \frac{\sum_j P(Y_j = k|x_j,\lambda_t)}{m} \]
\(m\) is the number of training examples
Animation of fitting
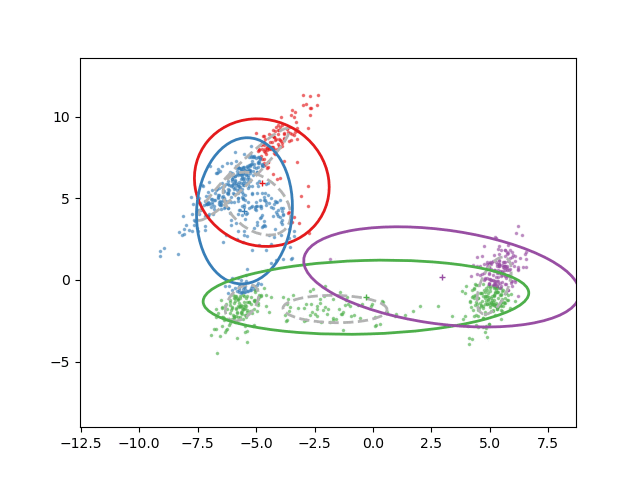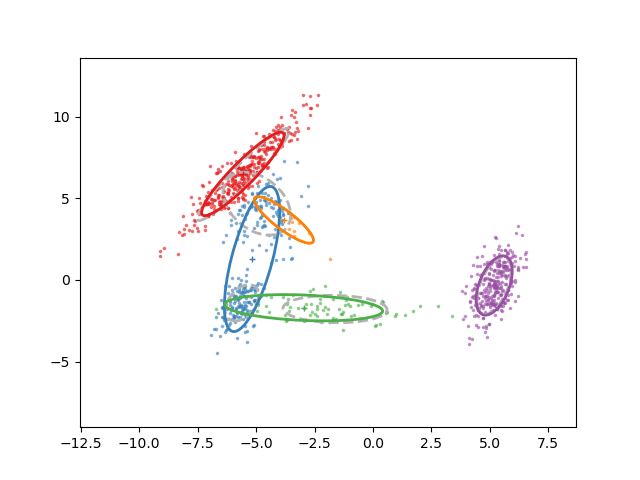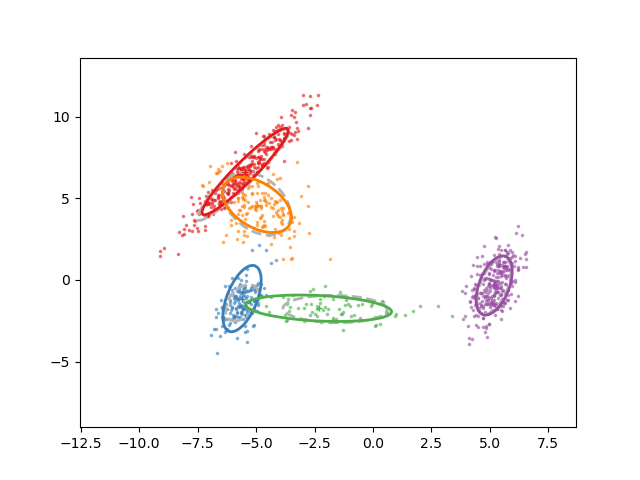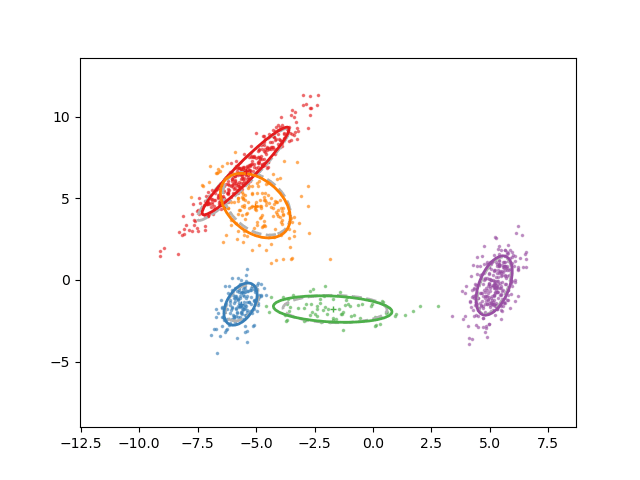
EM for GMMs: only learning means
On the \(t\)’th iteration let our estimates be: \(\lambda_t = \{ \mu_1^{(t)}, \mu_2^{(t)} ... \mu_K^{(t)} \}\)
E-step
Compute “expected” classes of all datapoints
\[P(Y_j = k|x_j, \mu_1 ... \mu_K) \propto \exp(-\frac{1}{2\sigma^2}\|x_j - \mu_k\|^2)P(Y_j = k)\]
M-step
Compute most likely new \(\mu\)s given class expectations
\[\mu_k = \frac{\sum_{j=1}^{m} P(Y_j = k|x_j) x_j}{\sum_{j=1}^{m} P(Y_j = k|x_j)}\]
What if we do hard assignments?
On the \(t\)’th iteration let our estimates be \(\lambda_t = \{ \mu_1^{(t)}, \mu_2^{(t)} ... \mu_K^{(t)} \}\)
E-step
Compute “expected” classes of all datapoints
\[P(Y_j = k | x_j, \mu_1...\mu_K) \propto \exp(-\frac{1}{2\sigma^2}\|x_j - \mu_k\|^2)\]
What if we do hard assignments?
On the t’th iteration let our estimates be \(\lambda_t = \{ \mu_1^{(t)}, \mu_2^{(t)} ... \mu_K^{(t)} \}\)
M-step
Compute most likely new \(\mu\)s given class expectations \[\mu_k = \frac{\sum_{j=1}^m \delta(Y_j=k,x_j)x_j}{\sum_{j=1}^m \delta(Y_j=k,x_j)}\]
\(\delta\) represents hard assignment to “most likely” or nearest cluster
Equivalent to k-means clustering algorithm!
Implementation
sklearn.mixture.GaussianMixture implements GMMs within sklearn.
GaussianMixturecreates the classn_componentsindicates the number of Gaussians to use.covariance_typeis type of covariancefullsphericaldiagtiedmeans all components share the same covariance matrix
max_iteris EM iterations to use
- Functions
M.fit(X)fits using the EM algorithmM.predict_proba(X)is the posterior probability of each component given the dataM.predict(X)predict the class labels of each data point
Review
Reading & Resources
Review Questions
- What are two ways in which GMMs give different results from K-means?
- What does it mean to say GMMs produce “soft assignments”?
- What can you say about a multivariate normal distribution with only diagonal elements?
- What does it mean to say a GMM is a generative model?
- Can mixture models be produced from distributions other than a Gaussian? If so, how is the distribution defined within the model? If not, why?
- Can GMMs describe clusters of non-Gaussian shapes? (Think of the moon example from lecture.) Describe.
- Can a GMM identify overlapping clusters? If so, what “signal” does it use in the data to distinguish these? If not, why not?
- A point lies equidistant between two clusters in a dataset. How do you expect this point to be clustered when using a GMM? How about with K-means?