Partial Least Squares Regression

Aaron Meyer (based on slides from Pam Kreeger)

Common challenge: Finding coordinated changes within data

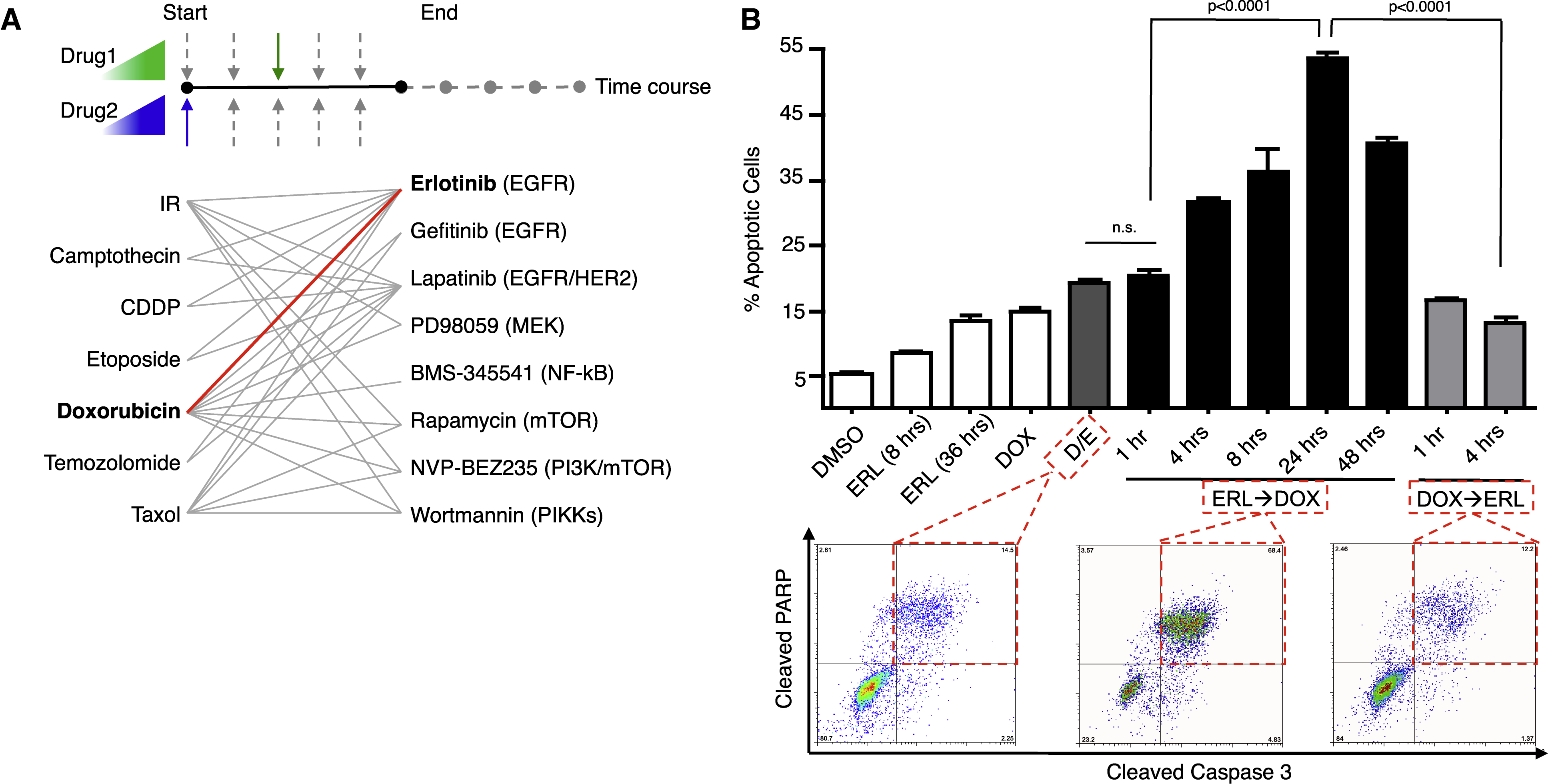
The timing and order of drug treatment affects cell death.

Notes about the methods today

  • Both methods are supervised learning methods, however have a number of distinct properties from others we will discuss.
  • Learning about PLS is more difficult than it should be, partly because papers describing it span areas of chemistry, economics, medicine and statistics, with differences in terminology and notation.

Regularization

  • Both PCR and PLSR are forms of regularization.
  • Reduce the dimensionality of our regression problem to \(N_{\textrm{comp}}\).
  • Prioritize certain variance in the data.

Principal Components Regression

Principal Components Regression

One solution: use the concepts from PCA to reduce dimensionality.

First step: Simply apply PCA!

Dimensionality goes from \(m\) to \(N_{comp}\).

Principal Components Regression

  1. Decompose X matrix (scores T, loadings P, residuals E) \[X = TP^T + E\]

  2. Regress Y against the scores (scores describe observations – by using them we link X and Y for each observation)

\[Y = TB + E\]

How do we determine the right number of components to use for our prediction?

A remaining potential problem

The PCs for the X matrix do not necessarily capture X-variation that is important for Y.

We might miss later PCs that are important for prediction!

Partial Least Squares Regression

The core idea of PLSR

What if, instead of maximizing the variance explained in X, we maximize the covariance explained between X and Y?

What is covariance?

PLSR is a cross-decomposition method

We will find principal components for both X and Y:

\[X = T P^t + E\]

\[Y = U Q^t + F\]

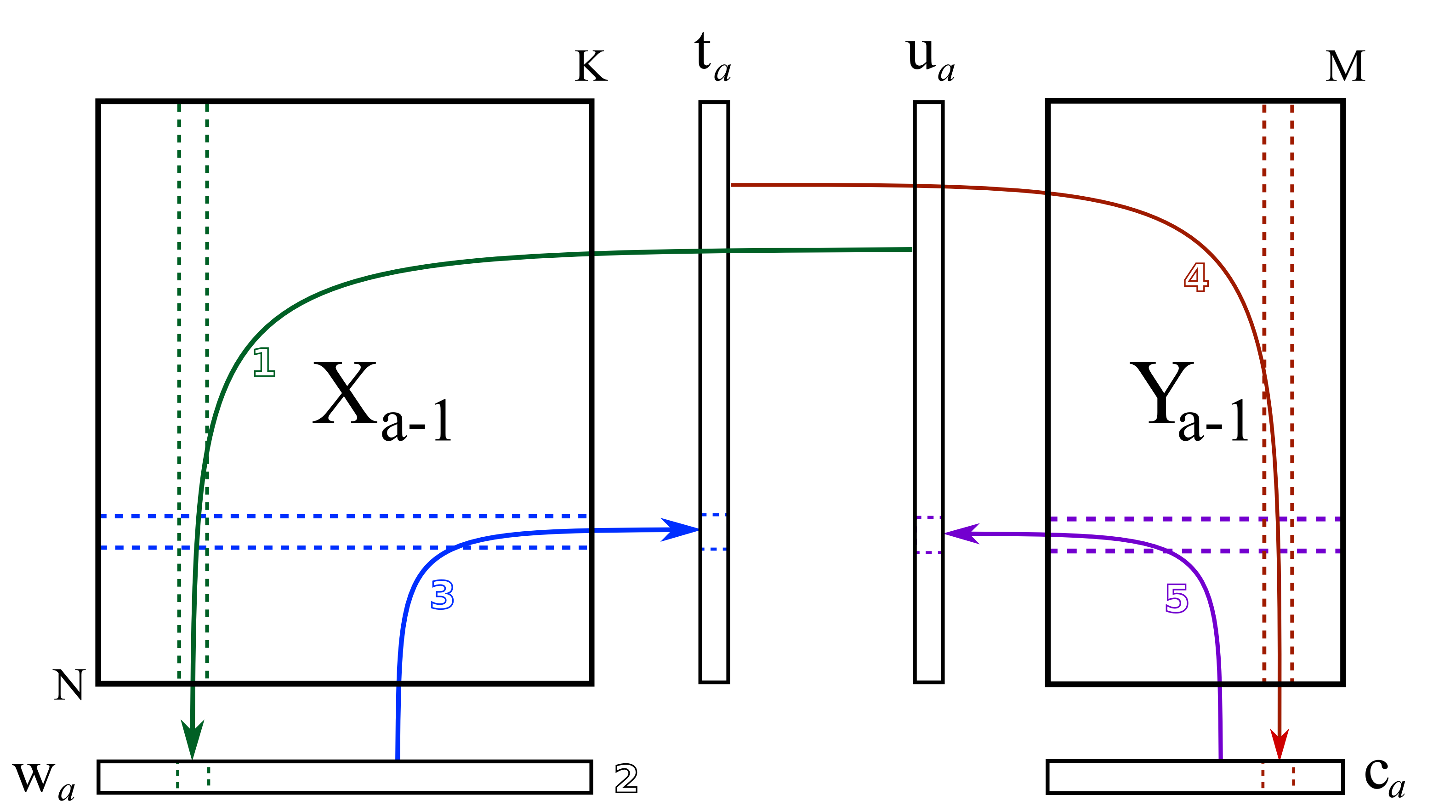
NIPALs while exchanging the scores

  1. Take a random column of Y to be \(u_a\), and regress it against X.

\[\mathbf{w}_a = \dfrac{1}{\mathbf{u}'_a\mathbf{u}_a} \cdot \mathbf{X}'_a\mathbf{u}_a\]

https://learnche.org/pid/latent-variable-modelling/projection-to-latent-structures/how-the-pls-model-is-calculated

NIPALs while exchanging the scores

  1. Normalize \(w_a\).

\[\mathbf{w}_a = \dfrac{\mathbf{w}_a}{\sqrt{\mathbf{w}'_a \mathbf{w}_a}}\]

https://learnche.org/pid/latent-variable-modelling/projection-to-latent-structures/how-the-pls-model-is-calculated

NIPALs while exchanging the scores

  1. Regress \(w_a\) against \(X^T\) to obtain \(t_a\).

\[\mathbf{t}_a = \dfrac{1}{\mathbf{w}'_a\mathbf{w}_a} \cdot \mathbf{X}_a\mathbf{w}_a\]

https://learnche.org/pid/latent-variable-modelling/projection-to-latent-structures/how-the-pls-model-is-calculated

NIPALs while exchanging the scores

  1. Regress \(t_a\) against Y to obtain \(c_a\).

\[\mathbf{c}_a = \dfrac{1}{\mathbf{t}'_a\mathbf{t}_a} \cdot \mathbf{Y}'_a\mathbf{t}_a\]

https://learnche.org/pid/latent-variable-modelling/projection-to-latent-structures/how-the-pls-model-is-calculated

NIPALs while exchanging the scores

  1. Regress \(c_a\) against \(Y^T\) to obtain \(u_a\).

\[\mathbf{u}_a = \dfrac{1}{\mathbf{c}'_a\mathbf{c}_a} \cdot \mathbf{Y}_a\mathbf{c}_a\]

https://learnche.org/pid/latent-variable-modelling/projection-to-latent-structures/how-the-pls-model-is-calculated

NIPALs while exchanging the scores

  1. Cycle until convergence, then subtract off variance explained by \(\widehat{\mathbf{X}} = \mathbf{t}_a\mathbf{p}'_a\) and \(\widehat{\mathbf{Y}}_a = \mathbf{t}_a \mathbf{c}'_a\).

https://learnche.org/pid/latent-variable-modelling/projection-to-latent-structures/how-the-pls-model-is-calculated

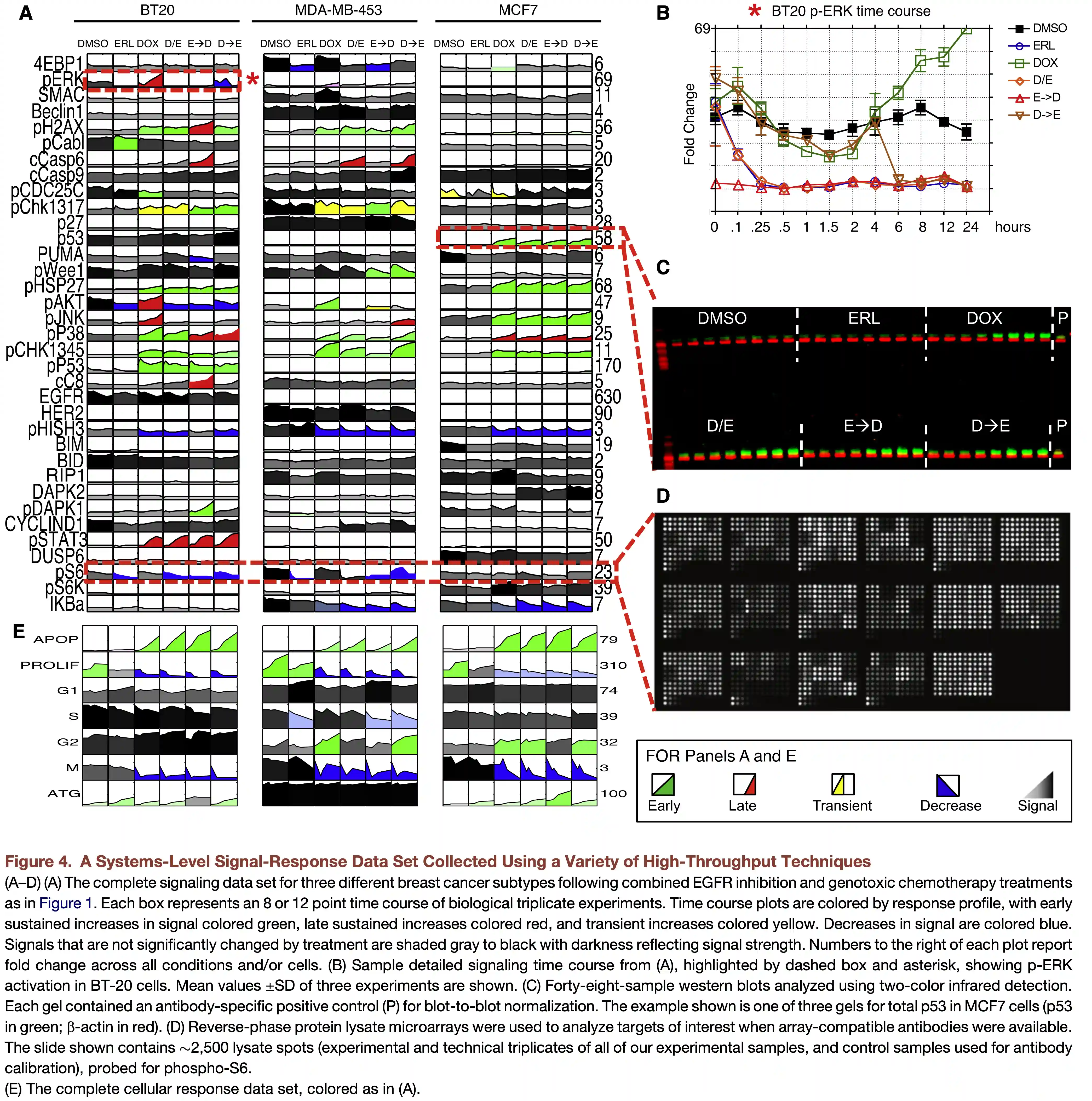
Components in PLSR and PCA Differ

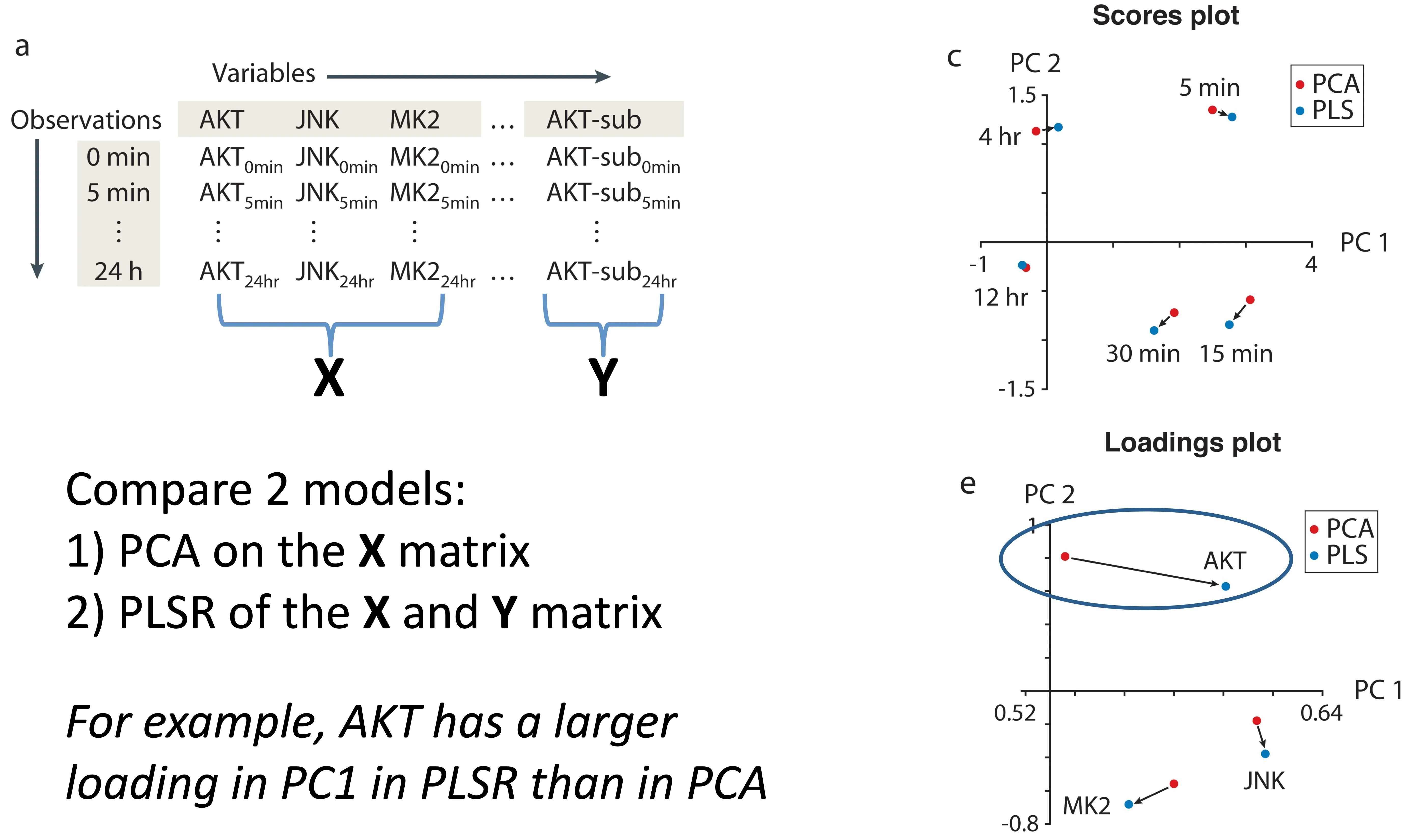
Janes et al, Nat Rev MCB, 2006

Determining the Number of Components

R2X provides the variance explained in X:

\[ R^2X = 1 - \frac{\lvert X_{\textrm{PLSR}} - X \rvert }{\lvert X \rvert} \]

R2Y shows the Y variance explained:

\[ R^2Y = 1 - \frac{\lvert Y_{\textrm{PLSR}} - Y \rvert }{\lvert Y \rvert} \]

If you are trying to predict something, you should look at the cross-validated R2Y (a.k.a. Q2Y).

PLSR uncovers coordinated cell death mechanisms

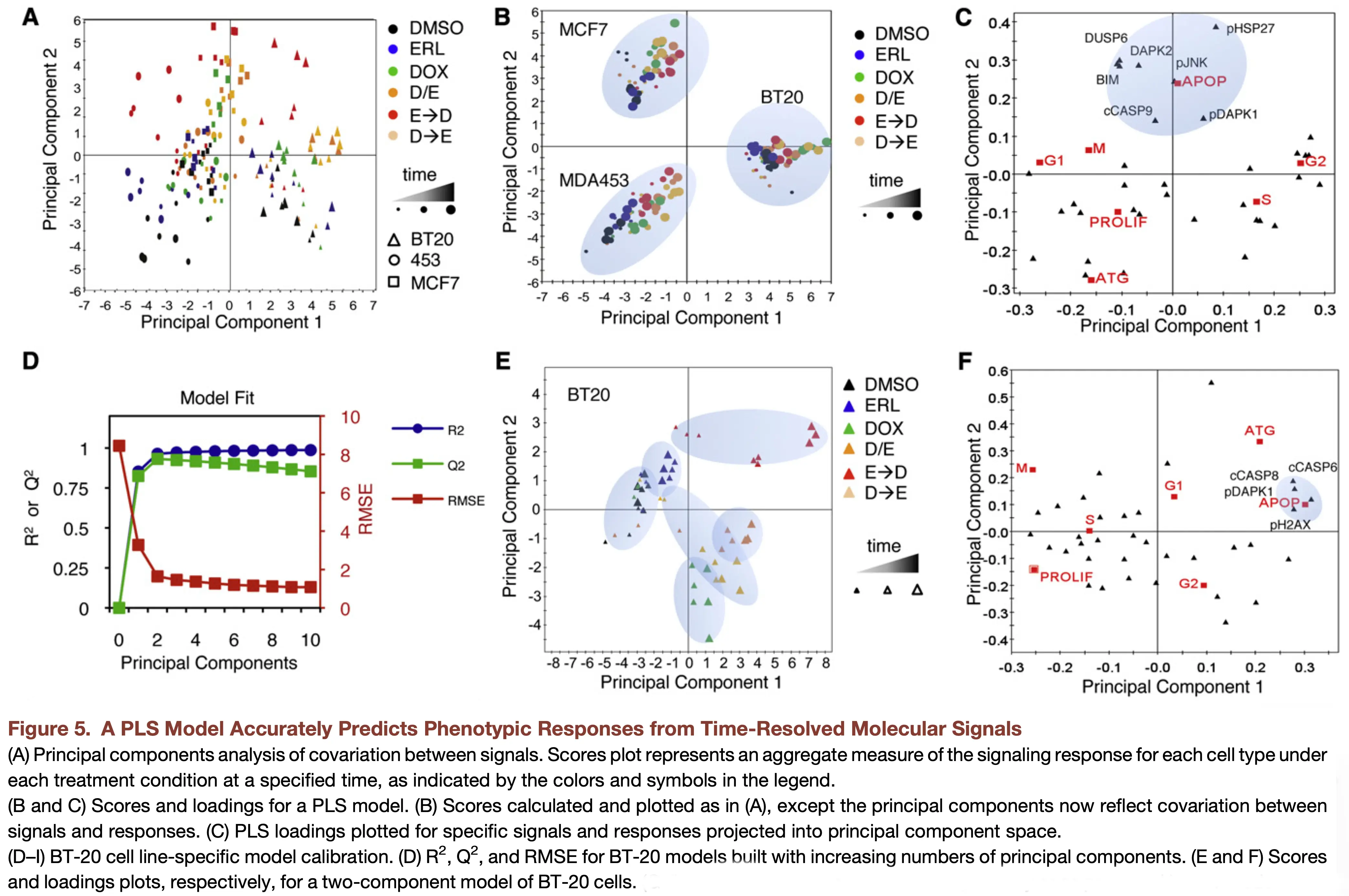
PLSR uncovers coordinated cell death mechanisms

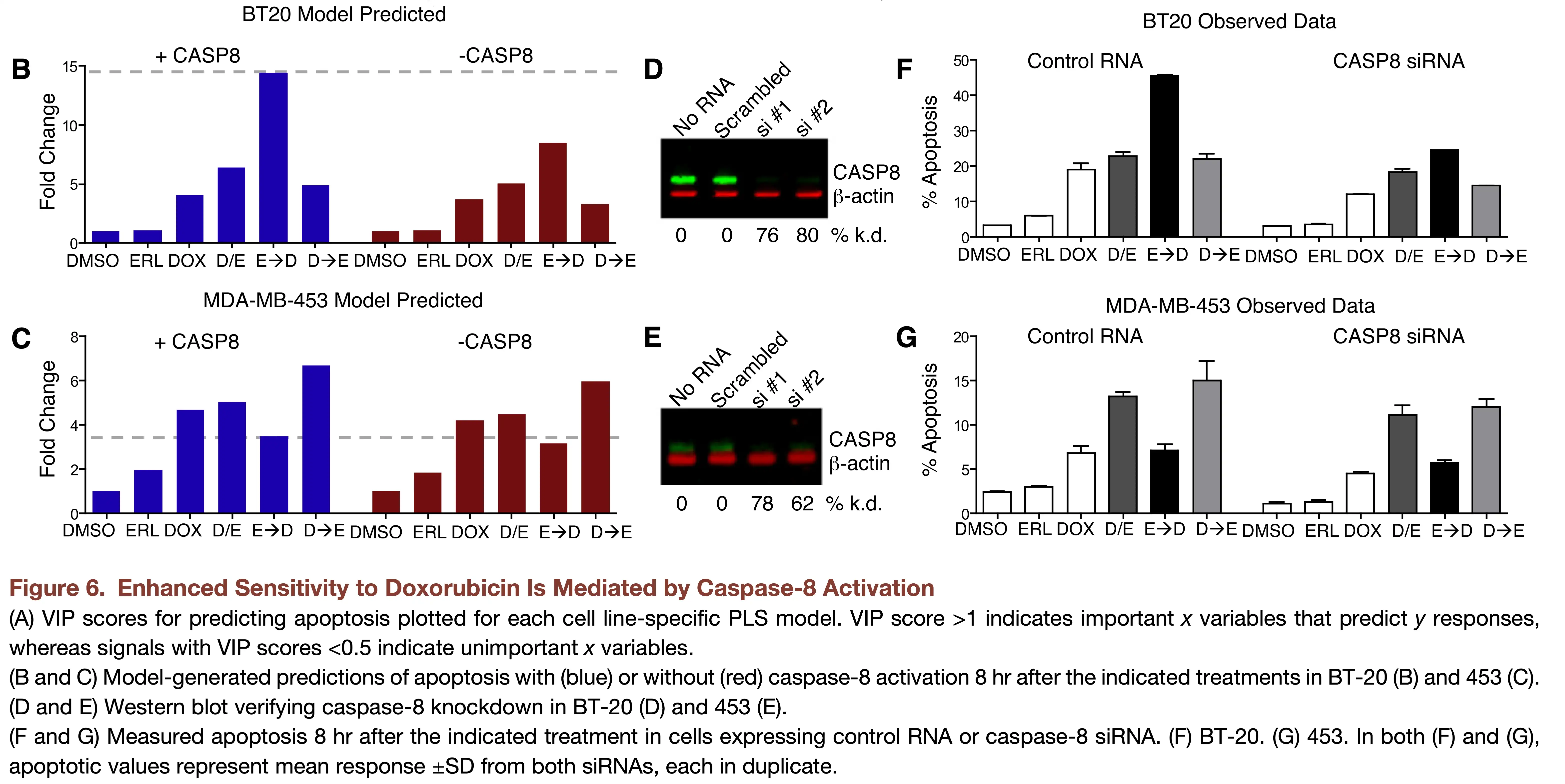
Practical Notes & Summary

PCR

PLSR

  • sklearn.cross_decomposition.PLSRegression
    • Uses M.fit(X, Y) to train
    • Can use M.predict(X) to get new predictions
    • PLSRegression(n_components=3) to set number of components on setup
    • Or M.n_components = 3 after setup

Comparison

PLSR

  • Maximizes the covariance
  • Takes into account both the dependent (Y) and independent (X) data

PCR

  • Uses PCA as initial decomp. step, then is just normal linear regression
  • Maximizes the variance explained of the independent (X) data

Performance

  • PLSR is amazingly well at prediction
    • This is incredibly powerful
  • Interpreting why PLSR predicts something can be challenging

Reading & Resources

Review Questions

  1. What are three differences between PCA and PLSR in implementation and application?
  2. What is the difference between PCR and PLSR? When does this difference matter more/less?
  3. How might you need to prepare your data before using PLSR?
  4. How can you determine the right number of components for a model?
  5. What feature of biological data makes PLSR/PCR superior to direct regularization approaches (LASSO/ridge)?
  6. Can you apply K-fold cross-validation to a PLSR model? If so, when do you scale your data?
  7. Can you apply bootstrapping to a PLSR model? Describe what this would look like.
  8. You use the same X data but want to predict a different Y variable. Do your X loadings change in your new model? What about for PCR?